Rappresentazione in virgola fissa e virgola mobile : capire le variabili Float

Devo dire la verità: delle variabili float (del modo in cui sono memorizzate/codificate) non ci ho mai capito un granchè fino a che non ho letto un bellissimo articolo scritto da Fabien Sanglard (autore del libro Game Engine Black Book : Wolfenstein 3D) in cui ha illustrato il sistema della codifica delle variabili float termini non convenzionali.

Ho trovato l’articolo di Fabien (Floating Point Visually Explained) talmente entusiasmante che non potevo non condividerlo con i miei lettori, sempre assetati di curiosità e anche perchè credo sia un elemento di base per noi a cui piace smanettare con l’arte della programmazione. Chiaramente nel seguente articolo c’è molto di mio e numerose aggiunte. Sedetevi comodi e, se volete, prendete anche carta, penna e calcolatrice come ho fatto io per poter fare delle prove (così potete anche segnalarmi se ho sbagliato qualcosa!).

Rappresentazione in virgola fissa

I computers possono utilizzare due sistemi per rappresentare i numeri reali (che, ricordiamo, sono i numeri interi e i numeri con decimali): virgola fissa e virgola mobile. La rappresentazione a virgola fissa è molto semplice: un certo numero di bytes verrà utilizzato per rappresentare la parte intera (e il segno), sappiamo che dopo questo numero di bytes ci sarà il punto decimale (la virgola), segue quindi un altro numero di bytes per rappresentare la parte decimale. Possiamo esprimere una codifica in virgola fissa come:

I.D

I numero intero che esprime la parte intera, D numero intero che esprime la parte decimale. Stabiliamo noi, a priori, di quanti bytes possono essere le due parti. In questi termini si capisce perchè la “virgola è fissa” : si trova sempre nella stessa posizione. Quando qui, su Settorezero, sui microcontrollori facciamo dei “magheggi”, del tipo: moltiplichiamo un numero per 10/100/1000 per lavorare su un intero e poi recuperare la parte decimale alla fine, non stiamo facendo nient’altro che operare in virgola fissa!

Prendiamo ad esempio un numero reale qualsiasi dotato di decimali: 1.234, potremmo lavorarci sul microcontrollore trattandolo come una variabile float, ma molto spesso non lo facciamo perchè sappiamo benissimo cosa accade: la memoria programma e la memoria dati consumata aumentano considerevolmente e diminuiscono anche le prestazioni (i calcoli con le variabili float sono lenti se eseguiti in emulazione come accade sui microcontrollori). Quindi in questi casi, in genere cosa facciamo? Operiamo in virgola fissa: prendiamo il numero, lo moltiplichiamo per 1000, in modo da ottenere 1234, facciamo tutte le operazioni che dobbiamo fare e alla fine dividiamo di nuovo per mille separando i vari “pezzi” del numero per poterli mostrare, ad esempio, su un display. Chiaramente questo sistema, seppur molto semplice e alla portata di sistemi con ridotte prestazioni, ha i suoi limiti: in questo esempio abbiamo moltiplicato per 1000 ma valeva soltanto per quel numero in particolare… se nel corso del programma abbiamo bisogno di altri numeri con un diverso quantitativo di decimali? Capite che le cose incominciano a complicarsi e in molti casi siamo costretti a fare numerose approssimazioni con conseguente perdita di precisione. Sia ben chiaro che la perdita di precisione in molte applicazioni è accettabile, ma in altre purtroppo no. Per questo motivo esiste la virgola mobile.

Rappresentazione in virgola mobile

L’aritmetica in virgola mobile permette ai computers di operare sulle variabili Float (generalmente a 32 bit), Double (generalmente 64 bit) e a salire. Indicherò queste variabili semplicemente come Float.

La codifica dei numeri Float è stabilita dalla normativa IEEE 754, non è l’unica normativa che stabilisce dei criteri per la virgola mobile ma è quella attualmente più utilizzata.

Qui prendo spunti dall’articolo di Fabien Sanglard citato all’inizio, per cui noterete che alcune cose sono spiegati con termini completamente diversi da come si fa sui libri dell’università: alla fine capirete che i concetti sono praticamente gli stessi, per cui mentre leggete, voi che già sapete, non vi scandalizzate.

Partiamo innazitutto dalla formula canonica che esprime la codifica dei numeri in virgola mobile:

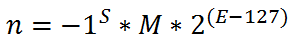
In questa formula S è il Segno (che determina se il numero è negativo o positivo!), M è la Mantissa, che esprime la parte decimale del numero, il 2 rappresenta la Base ed infine tutto il valore (E-127) è l’Esponente (il valore -127 si chiama Bias e serve per esprimere valori negativi, vedete che quando E vale meno del bias, l’esponente è negativo ⇒ viene fuori un numero minore di 1).

Il sistema è praticamente uguale alla notazione scientifica che usiamo normalmente con le calcolatrici in cui i numeri vengono scalati con potenze di 10 : 1.2345 * 10^-5 ad esempio. La differenza è che un computer non può usare le potenze di 10 dato che i numeri sono memorizzati in forma binaria, per cui la base è 2 anzichè 10. Gli umani usano la base 10 perchè è più congeniale avendo imparato a contare sulle dita delle mani.

Per capire meglio, in questa prima istanza, scriviamo la [1] in un’altra forma che ci aiuterà a capire meglio alcuni concetti:

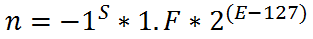
Vedete che ho sostituito M con 1.F: la nomenclatura è la stessa, sia M che 1.F vengono chiamate Mantissa. F viene anche detto parte frazionaria o semplicemente frazione. Ma usare quest’altra forma aiuta a non fare confusione successivamente dato che per adesso procediamo tralasciando alcune cose che riprenderemo poi.

Le 3 variabili della [2] (S,F ed E) vengono memorizzate, nel caso di una variabile Float a 32 bit (detta anche variabile float a precisione singola, per distinguerla da quella a precisione doppia, o Double, a 64 bit), in questo modo:

• 1 bit per il segno 
• 8 bit per il valore E della formula (da cui verrà sottratto il bias, 127, per ricavare l’Esponente con il segno)
• 23 bit per il valore F (che in fase di decodifica dovrà essere diviso per il numero di bit con cui è codificata la mantissa, 23 nel caso di variabili a precisione singola, ma vedremo dopo)

La parte segno è la più facile da capire: il bit di segno varrà zero se il numero è positivo, 1 se negativo (lo vediamo anche dalla formula: un numero qualsiasi elevato a zero fornisce 1, per cui tutta l’espressione risulterà positiva, se invece il valore -1 lo eleviamo ad 1, il risultato sarà -1 per cui tutta l’espressione risulterà negativa).

Adesso cerchiamo di capire come può un numero decimale essere codificato nei restanti 31 bit.

Spiego dapprima la parte E. Immaginiamo che la parte E rappresenti un gruppo di intervalli di potenze di 2 a partire da 0 ÷ (2^-127) fino ad arrivare all’intervallo (2¹²⁷) ÷ (2¹²⁸). Nel seguente disegno, per semplicità abbiamo messo soltanto i numeri interi, ma sappiate che il primo intervallo va da 0 a 2^-127 (ovvero un numero bassissimo: 0,(39 zeri)5877…) per cui l’intervallo 0÷1 non esiste (li in mezzo ci sono tantissimi altri intervalli!), ma esistono l’intervallo 1÷2 (ovvero 2⁰÷2¹), l’intervallo 2÷4(2¹÷2²) e così via:

Abbiamo cioè tanti intervalli di potenze di 2 successive in cui il primo numero dell’intervallo è compreso nell’intervallo stesso, mentre l’ultimo no (perchè appartiene all’inizio dell’intervallo successivo): quindi da 1 a 2 (1 compreso, 2 non compreso), da 2 a 4 (2 compreso, 4 non compreso), da 4 a 8 e così via (usando una notazione matematica comune potremmo scriverli come [1,2),[2,4),[4,8) ecc), fino ad arrivare all’ultimo intervallo che va da 2¹²⁷ fino a 2¹²⁸ (2¹²⁸ sempre non compreso: ha un utilizzo speciale, vedremo dopo): tenete conto della formula in cui abbiamo 2^(E-127) in cui, essendo E un numero ad 8 bit può variare da 0 a 255.

Il valore E in pratica serve a specificare in quale intervallo (dall’intervallo numero 0 a fino al 255°) si trova il nostro numero. Facciamo un esempio concreto utilizzando un numero reale: 6.1

Innanzitutto dobbiamo capire in quale dei tanti intervalli capita! Capita sicuramente nell’intervallo 4÷8 (2²÷2³), prendiamo come riferimento il primo numero dell’intervallo (4) e lo trasformiamo in potenza di 2 (2²) e prendiamo solo il valore della potenza (2) quindi l’esponente (tutta la parte (E-127) della formula) deve valere 2 per cui il solo valore E vale:

2=(E-127) ⇒ E=2+127=129.

Rimane da codificare la restante parte da aggiungere al numero individuato da E. La parte decimale, nella [2], viene espressa dalla Mantissa. La parte F della mantissa (ricordate 1.F nella [2]) può essere immaginata come un valore di offset (da 0 a 1, con 1 non compreso, così che tutta la Mantissa va in un range da 1 a 2 non compreso) all’interno dell’intervallo stabilito da E: abbiamo capito che il numero che vogliamo codificare deve capitare in un preciso intervallo di potenze di 2: se il numero preso ad esempio fosse stato 6, sarebbe capitato precisamente in mezzo tra 4 e 8 per cui l’offset sarebbe valso 0.5 (ricordo deve andare da 0 a 1 non compreso), se il numero preso ad esempio era 4 l’offset sarebbe stato 0 perchè il numero capita proprio all’inizio dell’intervallo.

Il nostro numero è invece 6.1, quindi l’offset è leggermente più spostato a destra rispetto alla metà dell’intervallo tra 4 e 8 (che vale 6): ecco la F serve ad esprimere questo offset all’interno del range stabilito da E. Vediamo di capirlo meglio con un disegno:

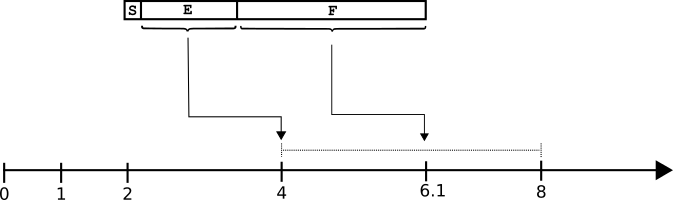
Il valore E ci ha fatto individuare l’intervallo (4÷8 perchè 6.1 cade tra 4 e 8), il valore F ci aiuterà a codificare in quale punto preciso dell’intervallo cade la restante parte che serve a completare il numero.

6.1 è posizionato nell’intervallo 4÷8 (quasi al centro, ha quindi un offset leggermente più grande di 0.5) e precisamente nel punto: 

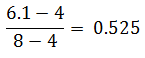
Capiamo che la Mantissa varrà 1.525 (dato che la dobbiamo scrivere come 1.F).

Nella [2] il valore F serve ad esprimere questo 0.525, in questo caso è riportato come decimale (come offset da 0 a 1 non compreso), per poterlo scrivere nel campo F della variabile float, dobbiamo riportarlo in un valore di offset a 23 bit (da 0 a 8388608): basta fare semplicemente: 0.525*(2²³)= 4404019.2. Dobbiamo purtroppo tralasciare la parte decimale e prendere soltanto la parte intera: 4404019.

Rimane il segno, che abbiamo messo per ultimo: essendo il numero positivo, il bit S varrà zero. 6.1 quindi avrà:

• S=0
• E=129
• F=4404019

Esprimendo questi valori in binario:

1. S=0
2. E=10000001
3. F=1000110011001100110011

Quindi il nostro 6.1, codificato come float, verrà memorizzato in 32 bit in questa forma:

Che in esadecimale è 40C33333 (occhio! intendo in esadecimale come se non stessimo tenendo conto che il numero è un float anzichè un intero!).

Adesso proviamo a fare l’operazione inversa: ci hanno dato il numero esadecimale 40C33333 dicendo che è codificato come float. Aiutandoci con la calcolatrice di Windows (in modalità programmatore) ricaviamo subito le tre parti del numero float: S=0, E=129 e F=4404019. Vogliamo quindi trovare il numero float come è stato memorizzato. Facendo riferimento alla formula 1, abbiamo:

• -1^S = -1⁰ = 1 ⇒ il numero è positivo
• E=129 ⇒ 2^(129-127) = 2² per cui il numero cade nell’intervallo che va da 4 (2²) alla potenza di 2 successiva a 4, ovvero 8 (2³).
• La Mantissa, che è codificata con 23 bit, ci dice che dobbiamo dividere lo spazio tra 4 e 8 in 2²³ intervalli (8388608) e quindi prendere il 4404019° intervallo (il valore di F) per sapere in quale punto capita l’offset: 4404019/8388608=0.52499997. Aggiungiamo in testa il bit implicito (1) (ricordate che nella [2] la mantissa l’ho scritta come 1.F) e otteniamo: 1.52499997

Il numero, decodificato, vale pertanto: 1*1.52499997*4=6,099999

Come vedete non viene fuori 6.1 preciso ma con una buona approssimazione (tenete conto anche che nel primo passaggio abbiamo dovuto tralasciare un decimale e che ci sono altre approssimazioni dovute alla precisione del metodo), generalmente si tiene conto dei decimali di una variabile a precisione singola fino alla sesta/settima cifra: le restanti cifre sono dovute all’approssimazione del metodo utilizzato. Se vi serve precisione maggiore esistono i float a 64 bit e ancor più, ma anche in questi, inevitabilmente, alla fine ci saranno decimali che noi non abbiamo messo, per questo motivo i matematici finanziari in genere non utilizzano la codifica a virgola mobile.

Noterete anche che quando si tratta di numeri molto piccoli (quelli che cadono nel primo intervallo, ovvero 0÷2^-127) la precisione è maggiore (provate a dividere 2^-127 in 8388608 intervalli!), man mano che si sale, la precisione diminuisce.. anche se nel caso del primo intervallo abbiamo una situazione particolare:

Numeri denormalizzati

Chiaramente per iniziale semplicità di esposizione ho tralasciato delle cose, ma i più attenti avranno notato delle stranezze che ora spiego. Come vedete, della formula, la Mantissa l’ho espressa come 1.F. In realtà non è sempre così. Nella codifica IEEE-754 i numeri che hanno la mantissa espressa come 1.F (ovvero la Mantissa è un numero da 1 compreso a 2 non compreso) vengono definiti Normalizzati, questi numeri vengono codificati sempre con un esponente maggiore di -127 (ovvero E diverso da zero).

Diciamo che il computer quando vede che il valore E è diverso da zero, aggiunge l’1-virgola davanti alla frazione (F/2²³). Nel momento in cui il valore E vale zero (e quindi tutto l’esponente vale -127, ovvero il più piccolo valore possibile dell’esponente) i numeri così codificati vengono chiamati Denormalizzati o anche Subnormalizzati e il computer non aggiunge più l’1-virgola davanti al valore di F ma lo lascia come 0.nnnnn, la Mantissa rientra quindi nel range [0,1), questo sistema serve a rappresentare lo zero, che altrimenti non sarebbe rappresentabile. Capite che i numeri denormalizzati sono numeri piccolissimi disposti in un ristretto range intorno allo zero, da un lato e dall’altro.

L’utilizzo dei numeri denormalizzati causa errori di underflow perchè in questo range della Mantissa otteniamo numeri più piccoli della sensibilità ammessa da questo sistema e capita pertanto che in alcune operazioni si possano ottenere risultati talmente piccoli da non poter essere memorizzati e vengono quindi confusi con lo zero.

Casi speciali

A questo punto si capisce che con questo sistema abbiamo anche uno zero negativo e uno zero positivo dato che quando rappresentiamo lo zero con questo sistema, c’è sempre il bit di segno che possiamo mettere a zero o a uno restituendoci +0 e -0. Questa cosa a molti potrebbe apparire senza senso, ma in realtà un senso ce l’ha (diciamo che in un certo senso serve a far capire che siamo arrivati allo zero da sinistra o da destra). Ad ogni modo i due zero vengono trattati sempre come zero tranne nel caso di una divisione di un numero positivo per -0 in cui viene restituito il valore -∞.

Il sistema della virgola mobile lascia spazio anche ad altri tipi di non-numeri (passatemi il termine!): abbiamo i 2 valori ±∞ quando l’esponente vale 128 (ovvero E vale 255) e F vale zero (ovvero la mantissa vale 1). I valori di infinito vengono restituiti nei casi di overflow (esempio +∞ viene restituito nel caso di divisione per zero di un numero positivo), e abbiamo il NaN (Not A Number) quando l’esponente vale 128 e M è diverso da zero. Il NaN serve per restituire un valore quando si esegue un’operazione non consentita, ad esempio la radice quadrata di un numero negativo.

La FPU

I computer moderni sono dotati di una FPU (Floating Point Unit) che prende posto all’interno del processore (si chiama anche Co-Processore) ed è delegata ad eseguire esclusivamente tutti i calcoli in virgola mobile. In passato il coprocessore era un optional e poteva essere installato a parte con un costo aggiuntivo anche notevole (io vengo dall’epoca in cui le schede madri dei PC avevano lo zoccolo (quasi sempre vuoto!) per ospitare il coprocessore 287 o 387 affianco ai processori 286 e 386. Con l’avvento dei processori 486 (tranne il 486SX) il coprocessore è stato integrato. Anche altri processori, come alcuni della serie Motorola 68000 (quello utilizzato dall’Amiga) potevano avere come optional una FPU (il 68881 ad esempio).

I microcontrollori che utilizziamo generalmente non hanno una FPU integrata e i calcoli in virgola mobile vengono eseguiti mediante emulazione che, come dicevo in alto, richiede un dispendio esagerato di risorse. Esistono comunque microcontrollori dotati di FPU (come gli STM32L basati su architettura ARM).

Links

• Convertitore On-Line (divertitevi a scrivere un numero e vedere come viene codificato in float)
• Floating Point Visually Explained by Fabien Sanglard
• What every computer scientist should know about floating-point arithmetic
• Tutorial sulla rappresentazione dei dati
• Altro tutorial sull’aritmetica Floating Point