Capire come funzionano le numerazioni decimale, binaria, esadecimale e ottale. Funzioni in VB.NET e Add-In per Excel per convertire un numero da una base all’altra
La numerazione che utilizziamo normalmente, nella vita di tutti i giorni è a base 10, il che significa che utilizziamo 10 simboli (0,1,2,3,4,5,6,7,8,9) per esprimere una determinata “quantità” e che ogni “simbolo” (che chiamerò d’ora in poi “digit”) rappresenta una potenza di 10 a crescere da destra verso sinistra partendo da zero.
Spiego meglio questa cosa con degli esempi. Quando scriviamo, ad esempio, 123 in modalità decimale, abbiamo in realtà scritto 3 digits che rappresentano potenze di 10 a crescere:
123 = 3*(10^0) + 2*(10^1) + 1*(10^2)
Magari l’immagine spiega un po’ meglio l’operazione:
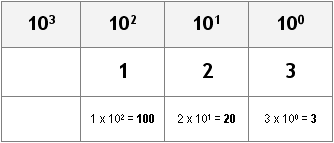
come vedete si prende un digit alla volta, partendo da destra, lo si moltiplica per la corrispondente potenza di 10 relativa alla sua posizione partendo da zero (prima posizione=0) e lo si somma con gli altri, altro esempio:
8023 = 3*(10^0) + 2*(10^1) + 0*(10^2) + 8*(10^3)

Ricordo che un qualsiasi numero elevato ad una potenza di zero, vale 1. E’ in pratica la stessa cosa che facevamo alle elementari con le bacchettine colorate che rappresentavano unità, decine, centinaia, migliaia… Ricordate?Anzichè scrivere 100 stiamo scrivendo 10^2 … Non cambia nulla, non vi spaventate!
Questo concetto, che dovrebbe risultare abbastanza “maneggevole” una volta appreso bene il meccanismo, anche se apparentemente “elementare” ci permette di ragionare con un certo meccanismo di base e di capire come funzionano le numerazioni in altre basi:
La numerazione binaria (ovvero a base 2), ad esempio, utilizza soltanto 2 simboli (0 e 1) e ogni digit rappresenta una potenza di 2:
10100 = 0*(2^0) + 0*(2^1) + 1*(2^2) + 0*(2^3) + 1*(2^4) = 20 (in decimale)
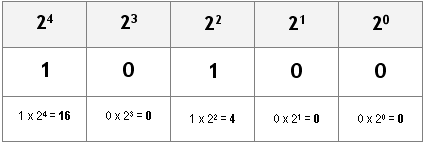
Come vedete non cambia nulla: il concetto è lo stesso: base 10 = 10 simboli e potenze di 10, base 2= 2 simboli e potenze di 2. Andiamo avanti.
La numerazione esadecimale (ovvero a base 16) fa invece uso di 16 simboli (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F) e ogni digit rappresenta una potenza di 16, in questo caso capisco che alcuni non hanno familiarità a trattare le 6 lettere come numeri.. ma basta ricordare semplicemente che in realtà la lettera A (esadecimale) vale 10 (decimale), la lettera B vale 11 ecc. ecc. fino ad arrivare ad F che vale 15.
Esempio:
E3B = 11*(16^0) + 3*(16^1) + 14*(16^2) = 3643 (in decimale)

Il succo non cambia: ricordiamoci che alla E va sostituito 14, alla B va sostituito 11 ecc e che le potenze devono essere potenze di 16….
Altra numerazione diffusa (anche se poco) è la numerazione ottale (a base 8), che fa uso di 8 simboli (0,1,2,3,4,5,6,7) e ogni digit rappresenta una potenza di 8. Il meccanismo di conversione da base ottale a decimale non cambia… Lascio fare a voi delle prove ;) Avete la calcolatrice di Windows per verificare che state operando correttamente: basta visualizzarla in modalità scientifica e passare da una base all’altra selezionando le apposite opzioni:
![]()
Tenete conto che esiste addirittura la numerazione sessagesimale (ovvero a base 60!, che fa uso cioè di 60 simboli e potenze di 60)… Dove viene usata? Avete presente la misurazione di latitudine, longitudine oppure la misurazione degli angoli in gradi? In questo nostro articolo potete saperne di più anche sulla numerazione a base 60.
Ma perchè esistono questi tipi di numerazione?
Tutto nasce da esigenze di comodità o compattezza nel rappresentare una determinata quantità.
La numerazione decimale è in realtà la più comoda per gli esseri umani, perchè siamo stati abituati a ragionare in questo modo dall’antichità e ci è quindi la più familiare. Si dice che il motivo stia probabilmente nel fatto che si è sempre cominciato a contare utilizzando le mani, e dal momento che le mani hanno 10 dita…
La numerazione binaria è quella invece utilizzata dai computer attuali e dalle apparecchiature elettroniche digitali in generale, che possono ragionare soltanto su due stati: 0=spento (o OFF o FALSE), 1=acceso (o ON o TRUE). In questo caso ogni digit viene più propriamente chiamato Bit, i Bit generalmente vengono raggruppati in blocchi di 8 i quali prendono il nome di Byte, un gruppo di 4 Bit viene invece chiamato Nibble.
La numerazione esadecimale è nata dall’esigenza di rappresentare in maniera più compatta i gruppi di Byte, difatti un byte rappresentato in binario, richiede massimo 8 digits, lo stesso byte rappresentato in decimale, può richiedere fino a 3 digits invece rappresentato in esadecimale può richiedere massimo 2 digits:
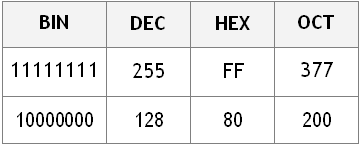
Difatti una cifra esadecimale corrisponde ad un Nibble (4 bit, cioè 4 cifre binarie) e due cifre esadecimali corrispondono ad un Byte (o due Nibble se preferite, 8 cifre binarie)
Nei software, per non creare confusione, i numeri espressi in esadecimale vengono rappresentati generalmente anteponendo 0x al numero (cioè nel software anzichè scrivere FF scriveremo 0xFF, anzichè scrivere 80 scriveremo 0x80, questa è ad esempio la convenzione utilizzata in C, in Java e altri linguaggi C-Like), in altri linguaggi si denota un numero esadecimale anteponendo &H (questo il caso di Visual Basic.NET). Questo per dire al software che il numero è stato scritto in esadecimale e non in decimale (i numeri, se non specificato, vengono sempre interpretati come decimali dalla maggior parte dei compilatori a meno che non si specifica diversamente), difatti come abbiamo appena visto se scriviamo 80 e non specifichiamo in che base l’abbiamo scritto, possono succedere bei problemi, perchè 80 in decimale vale appunto 80, ma in esadecimale vale 128!! In C ad esempio dovremo quindi scrivere in questo caso 0x80 (cioè 128), altrimenti se scriviamo 80 il software ragionerà proprio su 80.
Come si può anche intuire dall’immagine, una cifra ottale, invece, corrisponde a gruppi di 3 Bit.
Vediamo quindi come convertire i numeri da una base all’altra, il concetto di base per tutte le numerazioni è sempre lo stesso: basta ricordare che un numero in base Y deve utilizzare Y simboli e ogni digit deve rappresentare una potenza di Y da destra verso sinistra partendo da zero.
Illustrerò le funzioni di conversione scritte da me in VB.NET. Basta sapere la funzione dei seguenti operatori:
- MOD : serve a restituire unicamente il resto di una divisione (alcuni linguaggi utilizzano il simbolo % per fare la stessa funzione)
- / : divisione normale, che restituisce un risultato completo dei decimali
- \ : divisione intera, che restituisce soltanto la parte intera del risultato
Capito il concetto che sta alla base è semplice applicarlo a qualsiasi linguaggio di programmazione conoscendo le stesse funzioni relative al linguaggio preferito o creandosele se non esistono.
Assumo inoltre che X rappresenta il mio numero da convertire e premetto che alcune funzioni, utilizzando ABS (che restituisce il valore assoluto di un numero, messo giusto per sicurezza) hanno bisogno che venga importata la libreria System.Math con la direttiva Imports all’inizio del modulo/form. Tenete inoltre conto che le funzioni qui illustrate non hanno “protezione”, nel senso che, ad esempio, se passate un numero esadecimale da convertire con all’interno caratteri strani, sarà convertito ugualmente, così come se passate una cifra 8 o 9 in un numero ottale (un numero ottale non può contenere 8 e 9!)… Queste limitazioni al limite andranno messe ad esempio nei caratteri digitabili in una textbox se decidete di prendere l’input da tale controllo.
Indice dei contenuti
Conversione da decimale a binario
1. Calcolo il resto della divisione X / 2 (ovvero: X MOD 2). Il resto ovviamente potrà valere 1 oppure 0. Questo numero verrà aggiunto al risultato partendo da destra e andando verso sinistra.
2. Divido X per 2 prendendomi soltanto la parte intera e scartando i decimali (X = X\2)
3. Se dopo la divisione del punto 2 X vale zero, la conversione è finita, se non vale zero ritorno al punto 1 utilizzando il nuovo valore che ha assunto X
Public Function Dec2Bin(ByVal Decimal_Number As Long) As String Dim Result As String = "" ' Stringa che contiene il risultato Decimal_Number = Abs(Decimal_Number) ' Valore assoluto Do Result = CStr(Decimal_Number Mod 2) & Result ' Modulo (resto della divisione) Decimal_Number = Decimal_Number \ 2 ' Divisione intera Loop While Decimal_Number > 0 Return Result End Function |
Conversione da binario a decimale
Ogni numero (digit) che costituisce il valore binario rappresenta una potenza di 2, incominciando con 2^0 per il digit più a destra, 2^1 per quello appena successivo e così via.
Public Function Bin2Dec(ByVal Binary_Number As String) As Long Dim AD As String = "" Dim Result As Long = 0 For I As Integer = Len(Binary_Number) To 1 Step -1 ' Ciclo per estrarre un carattere alla volta, da destra verso sinistra AD = Mid(Binary_Number, I, 1) If AD = "1" Then Result = Result + 2 ^ (Binary_Number.Length - I) ' potenza di 2 End If Next Return Result End Function |
Conversione da decimale ad esadecimale
1. Calcolo il resto della divisione X / 16 (X MOD 16). Il resto sarà un numero da 0 a 15. Se il numero è maggiore di 9 devo convertirlo in lettera (10=A, 11=B, 12=C, 13=D, 14=E, 14=F). Il simbolo ottenuto verrà aggiunto al risultato da destra verso sinistra.
2. Divido X per 16 prendendomi soltanto la parte intera (X=X\16)
3. Se X vale zero, la conversione è finita, se non vale zero, ritorno al punto 1 utilizzando il nuovo valore che ha assunto X
Public Function Dec2Hex(ByVal Decimal_Number As Long) As String Dim Result As String = "" Dim Temp As Long = 0 Decimal_Number = Abs(Decimal_Number) Do Temp = Decimal_Number Mod 16 If Temp > 9 Then ' se il resto della divisione è superiore a 9 ' lo converto nella lettera sfruttando i codici ascii Result = Chr(64 + (Temp - 9)) & Result Else ' altrimenti lo resto così Result = CStr(Temp) & Result End If Decimal_Number = Decimal_Number \ 16 ' Divisione intera Loop While Decimal_Number > 0 Return Result End Function |
Conversione da esadecimale a decimale
Ogni numero (digit) che costituisce il valore esadecimale rappresenta una potenza di 16, incominciando con 16^0 per il digit più a destra, 16^1 per quello appena successivo e così via, tenendo conto che al posto di A si dovrà mettere 10, al posto di B 11 ecc.
Public Function Hex2Dec(ByVal Hexadecimal_Number As String) As Long Dim AD As String = "" Dim Result As Long = 0 Hexadecimal_Number = Hexadecimal_Number.ToUpper ' converto le lettere in maiuscole For I As Integer = Len(Hexadecimal_Number) To 1 Step -1 ' Ciclo per estrarre un carattere alla volta, da destra verso sinistra AD = Mid(Hexadecimal_Number, I, 1) If Not IsNumeric(AD) Then ' Se il carattere estratto non è un numero, ne ricavo il codice ascii ' e ci sottraggo il numero 55 per ottenere il valore corrispondente ' (A=10, B=11 ecc) AD = (Asc(AD) - 64 + 9) End If Result = (CInt(AD) * (16 ^ (Hexadecimal_Number.Length - I))) + Result ' potenza di 16 Next Return Result End Function |
Conversione da decimale a ottale e viceversa
Si usa sempre lo stesso sistema, tenendo conto che ci sono solo 8 simboli (da 0 a 7) e che le potenze sono di 8
Public Function Dec2Oct(ByVal Decimal_Number As Long) As String Dim Result As String = "" Dim Temp As Long = 0 Decimal_Number = Abs(Decimal_Number) Do Temp = Decimal_Number Mod 8 Result = CStr(Temp) & Result Decimal_Number = Decimal_Number \ 8 ' Divisione intera Loop While Decimal_Number > 0 Return Result End Function |
Public Function Oct2Dec(ByVal Octal_Number As String) As Long Dim AD As Integer = 0 Dim Result As Long = 0 ' Ciclo per estrarre un carattere alla volta, da destra verso sinistra For I As Integer = Len(Octal_Number) To 1 Step -1 AD = CInt(Mid(Octal_Number, I, 1)) Result = (AD * (8 ^ (Octal_Number.Length - I))) + Result ' potenza di 8 Next Return Result End Function |
Conversione da base y a base z
La cosa più semplice è sfruttare due funzioni successive passando per il decimale, da base y a decimale e quindi da decimale a base z.
Download
E’ possibile scaricare il modulo vb con già scritte tutte le funzioni e anche un addin excel che una volta installato, rende possibile utilizzare tali funzioni anche in un foglio Excel.
Scarica le funzioni di conversione tra basi numeriche per VB.NET:
[download#27]
Vai alla pagina con l’Add-In per Excel 2003 per convertire i numeri in varie basi numeriche