Basi della cartografia: convertiamo latitudine e longitudine da base60 a decimale. Il sistema sessagesimale e i suoi utilizzi pratici.

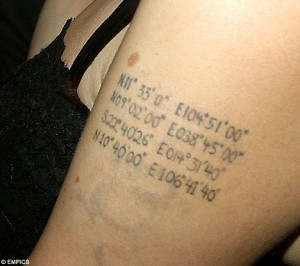Avete visto la foto qui a sinistra? Strano tatuaggio eh? Già… La ragazza in questione ha avuto un’idea molto originale: si è fatta tatuare sul braccio sinistro le coordinate geografiche dei luoghi in cui sono nati i suoi 4 figli. Di chi si tratta? Non vi distraete! Cerchiamo di capire piuttosto come si interpretano quei numeri, che è lo scopo di questo articolo.

Incominciamo innanzitutto con un po’ di basi di cartografia, giusto per rinfrescarci la memoria.

Le coordinate geografiche che ci permettono di risalire ad un punto esatto sulla superficie terrestre (ma non solo) sono una coppia di numeri che esprimono latitudine e longitudine.

La latitudine esprime la distanza angolare dall’equatore. L’equatore ha una latitudine di o°, il valore di latitudine aumenta man mano che ci avviciniamo ai poli , i quali hanno una latitudine di 90° (positiva per il polo Nord: +90°, negativa per il polo Sud: -90°).  I paralleli, ovvero le linee parallele all’equatore che troviamo generalmente disegnate sulle cartine geografiche, sui mappamondi ecc, non sono altro che punti aventi la stessa latitudine : i punti lungo uno stesso parallelo hanno quindi lo stesso valore di latitudine.

La longitudine, invece, esprime la distanza angolare dall’equatore al meridiano di Greenwich, il quale ha una longitudine di o°. La longitudine aumenta da 0° a 180° muovendosi dal meridiano di Greenwich al meridiano opposto. Il valore di longitudine è positivo verso est e negativo verso ovest.

Spero non vi siate spaventati… Ecco, un’immagine vale più di mille parole:

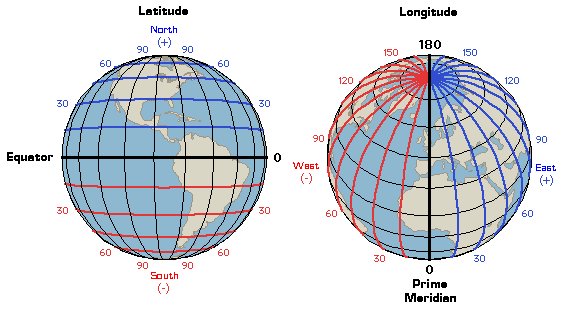
Dalle immagini vediamo chiaramente che i valori di latitudine vanno da 0° (equatore) a +90° (polo nord) e da 0° a -90° (polo sud).

I valori di longitudine invece vanno da 0° (primo meridiano, o meridiano di Greenwich) a 180° verso est, e da 0° a -180° verso ovest.

Incrociando quindi un meridiano e un parallelo (un valore di latitudine e un valore di longitudine) otteniamo quindi un punto sulla superficie terrestre.

Il sistema sessagesimale

I valori numerici con cui generalmente sono espressi latitudine e longitudine sono valori a base 60, ovvero utilizzano la notazione sessagesimale. Abbiamo già visto in un articolo precedente come funzionano le numerazioni in base 2, in base 16 ecc. In base 60 è più o meno la stessa cosa: i numeri andranno da 0 a 59, per rappresentare il 60 si utilizza un altro simbolo… Si ma come?

Faccio un esempio semplicissimo: il modo in cui esprimiamo un orario è in base 60! Arrivati a 59 secondi, non scriveremo 60 secondi ma scriveremo 1 minuto e 0 secondi, il minuto è il simbolo per rappresentare i 60 secondi, così come l’ora è il simbolo per rappresentare i 60 minuti. Questo esempio, che è alla portata di ogni giorno, dovrebbe essere abbastanza semplice da capire. Così come in base 2 (numerazione binaria) non possiamo avere simboli più grandi di 1, così come in base 16 (numerazione esadecimale) non possiamo avere simboli più grandi di 15, così in base 60 non possiamo avere simboli più grandi di 59.

In realtà la notazione che si utilizza per l’orario non è sessagesimale pura: difatti il sistema sessagesimale lo applichiamo soltanto ai minuti ed ai secondi: passate 24 ore (e non 60!) si parla di GIORNO, mentre i sottomultipli dei secondi vengono generalmente espressi in centesimi e non in sessantesimi.

La stessa, identica cosa, si fa per le misurazioni in gradi degli angoli: anche i gradi degli angoli vengono espressi con una numerazione in base 60, con la sola differenza che l’unità più grande anzichè chiamarsi ORA, si chiama GRADO, i sottomultipli invece si chiamano sempre minuto e secondo (o più correttamente: minuto primo e minuto secondo). Anche qui al di sopra del grado non abbiamo altri simboli, per tale motivo un valore di angolo può essere superiore a 60° (fino a 360 ovviamente, che è il massimo valore che un angolo può assumere).

Strana questa corrispondenza tra orario e angoli non trovate? Ma avete fatto caso che per leggere l’orario in realtà non si fa altro che interpretare l’angolo che le lancette formano con il numero 12 posto al vertice? Sempre di angoli si tratta ;)

Prendiamo adesso ad esempio il Colosseo, dove si trova, è facile dire: a Roma! Ma è più esatto fornire una coppia di coordinate per trovarne il punto preciso sul globo terrestre (come credete che faccia il TomTom a posizionare sulla sua mappa il colosseo proprio nel punto esatto in cui lo vedete?).

Le coordinate del colosseo sono:

41° 53’ 24″ N

12° 29’ 32″ E

e si leggono così: 41 gradi, 53 minuti primi e 24 secondi Nord (si tratta quindi del valore di latitudine, e ci troviamo quindi al di sopra dell’equatore) e 12 gradi, 29 minuti primi e 32 secondi Est (quindi questo è il valore di longitudine).

Spesso Nord ed Est si omettono e si utilizza invece il segno + davanti ai gradi per indicare Nord (per valore di latitudine) o Est (per longitudine), oppure il segno – per indicare Sud o Ovest.

Nota: nelle notazioni anglosassoni troveremo W (west) al posto di O (ovest)

A volte, invece, le coordinate anzichè essere espresse in sessagesimale, vengono espresse in decimale, e quindi le coordinate precedenti diventano:

41,89° N

12.49222° E

E’ sempre lo stesso punto sulla superficie terrestre, solo che l’abbiamo convertito da base 60 a base 10 (decimale). Le operazioni di conversione da base60 a base10 e viceversa sono semplicissime:

Convertire da sessagesimale a decimale

Vi spiego con degli esempi come si effettua la conversione. Supponiamo di avere un valore di latitudine di 82° 33′ 24″”

Prendiamo i gradi (82): rimarranno tal quali.

Prendiamo i minuti (33) e li dividiamo per 60 : 33/60 = 0,55

Prendiamo i secondi (24) e li dividiamo per 3600 : 24/3600 = 0,0066

Sommiamo le tre quantità e otteniamo il valore di gradi espresso in decimale : 82 + 0,55 + 0,006667 = 82,556667

Convertire da decimale a sessagesimale

Supponiamo di avere il valore 82,556667

Prendiamo la parte intera (82) : questo è il valore dei gradi

Prendiamo la parte decimale (0,556667) e la moltiplichiamo per 60 : 0,556667 * 60 = 33,40002

Di quest’ultimo valore prendiamo la parte intera (33) : questi sono i minuti

Prendiamo la restante parte decimale del valore precedente (0,40002) e moltiplichiamola per 60 : 0,396 * 60 = 24,0012 : questo è il valore dei secondi.

Ovviamente la precisione dipende dal numero di decimali che ci trasciniamo dietro durante le operazioni.

Da questo nostro articolo potete scaricare eseguibile e, se siete iscritti, codice sorgente di un piccolo applicativo in vb.net (framework 2.0) che effettua le operazioni di conversione qui descritte.

A proposito… Mica vi state ancora chiedendo a chi appartiene quel tatuaggio in cima all’articolo? Cliccate qui e lo scoprirete ;)